Explaining Predictions: Interpretable models (decision tree)
Introduction
This is a follow up post of using simple models to explain machine learning predictions. In the last post, we introduced logistic regression and in today’s entry we will learn about decision tree.
We will continue to use the Cleveland heart dataset and use tidymodels principles where possible. The details of the Cleveland heart dataset was also described in the last post.
#library
library(tidyverse)
library(tidymodels)
#import
heart<-read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/processed.cleveland.data", col_names = F)
# Renaming var
colnames(heart)<- c("age", "sex", "rest_cp", "rest_bp",
"chol", "fast_bloodsugar","rest_ecg","ex_maxHR","ex_cp",
"ex_STdepression_dur", "ex_STpeak","coloured_vessels", "thalassemia","heart_disease")
#elaborating cat var
##simple ifelse conversion
heart<-heart %>% mutate(sex= ifelse(sex=="1", "male", "female"),fast_bloodsugar= ifelse(fast_bloodsugar=="1", ">120", "<120"), ex_cp=ifelse(ex_cp=="1", "yes", "no"),
heart_disease=ifelse(heart_disease=="0", "no", "yes"))
## complex ifelse conversion using `case_when`
heart<-heart %>% mutate(
rest_cp=case_when(rest_cp== "1" ~ "typical",rest_cp=="2" ~ "atypical", rest_cp== "3" ~ "non-CP pain",rest_cp== "4" ~ "asymptomatic"), rest_ecg=case_when(rest_ecg=="0" ~ "normal",rest_ecg=="1" ~ "ST-T abnorm",rest_ecg=="2" ~ "LV hyperthrophy"), ex_STpeak=case_when(ex_STpeak=="1" ~ "up/norm", ex_STpeak== "2" ~ "flat",ex_STpeak== "3" ~ "down"), thalassemia=case_when(thalassemia=="3.0" ~ "norm",
thalassemia== "6.0" ~ "fixed", thalassemia== "7.0" ~ "reversable"))
# convert missing value "?" into NA
heart<-heart%>% mutate_if(is.character, funs(replace(., .=="?", NA)))
# convert char into factors
heart<-heart %>% mutate_if(is.character, as.factor)
#train/test set
set.seed(4595)
data_split <- initial_split(heart, prop=0.75, strata = "heart_disease")
heart_train <- training(data_split)
heart_test <- testing(data_split)
# create recipe object
heart_recipe<-recipe(heart_disease ~., data= heart_train) %>%
step_knnimpute(all_predictors())
# process the traing set/ prepare recipe(non-cv)
heart_prep <-heart_recipe %>% prep(training = heart_train, retain = TRUE)
# model building
dt_model<-decision_tree( min_n = 20, tree_depth = 30, mode = "classification") %>% set_engine("rpart") %>% fit(heart_disease ~ ., data = juice(heart_prep))Decision tree
Genesis of the tree
A decision tree splits the dataset into smaller subgroups called nodes. The split is based on the most significant feature such that the nodes are as distant as possible from each other and the observations within the nodes are homogenous as possible. The decision tree continues this recursive algorithm to find the next significant feature to split into the nodes to grow the tree. The splitting continues until a stop criterion is met.
Nodes
Nodes at different level of the tree have different pre-fixes.
Root node is the first node at the top of the tree and it represents the entire dataset. Being the first node of the tree also means it’s the first node in the entire tree to be split.
Terminal nodes (or terminal leaves) are the end of the tree. They do not split any further as the recursive algorithm to continue splitting has come to a stop. The maximum number of terminal nodes in a tree is 2 to the power of the tree depth.
Nodes in between the root and terminal node are called intermediate nods/ internal nodes/split nodes.
The connection between nodes are called branches.
Splitting of node
There are multiple approaches to determine which feature to split the node. The 2 common techniques are:
Information Gain (a derivate of Entropy) Information gain tells us how much information a feature tells us about the prediction. The larger the information gain, the more informative the feature can inform us about the prediction which allows us to split the parent node such that the predictions within the children nodes are homogenous as possible. As observations in terminal nodes are purely homogenous, the feature resulting in that split is the most informative and therefore has the largest information gain (which is 1).
Gini Impurity/ Gini Index. Impurity is the likelihood of being INCORRECT if you randomly assign a predictor class to an observation in the node. Thus, the larger the Gini Impurity, the more impure the nodes are and the less likely the observations in the nodes are alike. However, we want the observations in the nodes to be as similar as possible. Thus, the split will minimize the Gini Impurity. The decision tree package
rpartwhich we will use, splits by the gini index by default. The splitting index can be changed to information gain.
Other techniques to split nodes include: Chi-Square and Variance Reduction.
Stopping the splits
The follow parameters will terminate of growth of the tree.
- Cost complexity criterion: helps to identify the smallest pruned tree/ most optimal subtree that has the lowest penalized error. Smaller penalties tend to produce more complex models.
- Minsplit: minimum number of observations needed to split a parent node else it will be forced to create a terminal node. The default in
rpartis 20. - Maxdepth: maximum number of internal nodes. The default in
rpartis 30.
These parameters can also be used to tune the model to boost performance. In this post, the default parameters were used, just that I made them explicit.
Plotting the tree
The decision tree plot was created with rpart.plot::rpart.plot. Incomplete plots were created when I passed the model to general plot and text functions.
rpart.plot::rpart.plot(dt_model$fit,
#explicitly label the criteria for each node instead of default type 2 which labels yes/no
type=4,
# display the number and percentage of obs in the node
extra = 101,
branch.lty=3,
#display the node numbers
nn=TRUE,
# If roundint=T, will display warning "Cannot retrieve the data used to build the model (so cannot determine roundint and is.binary for the variables)"
roundint=F)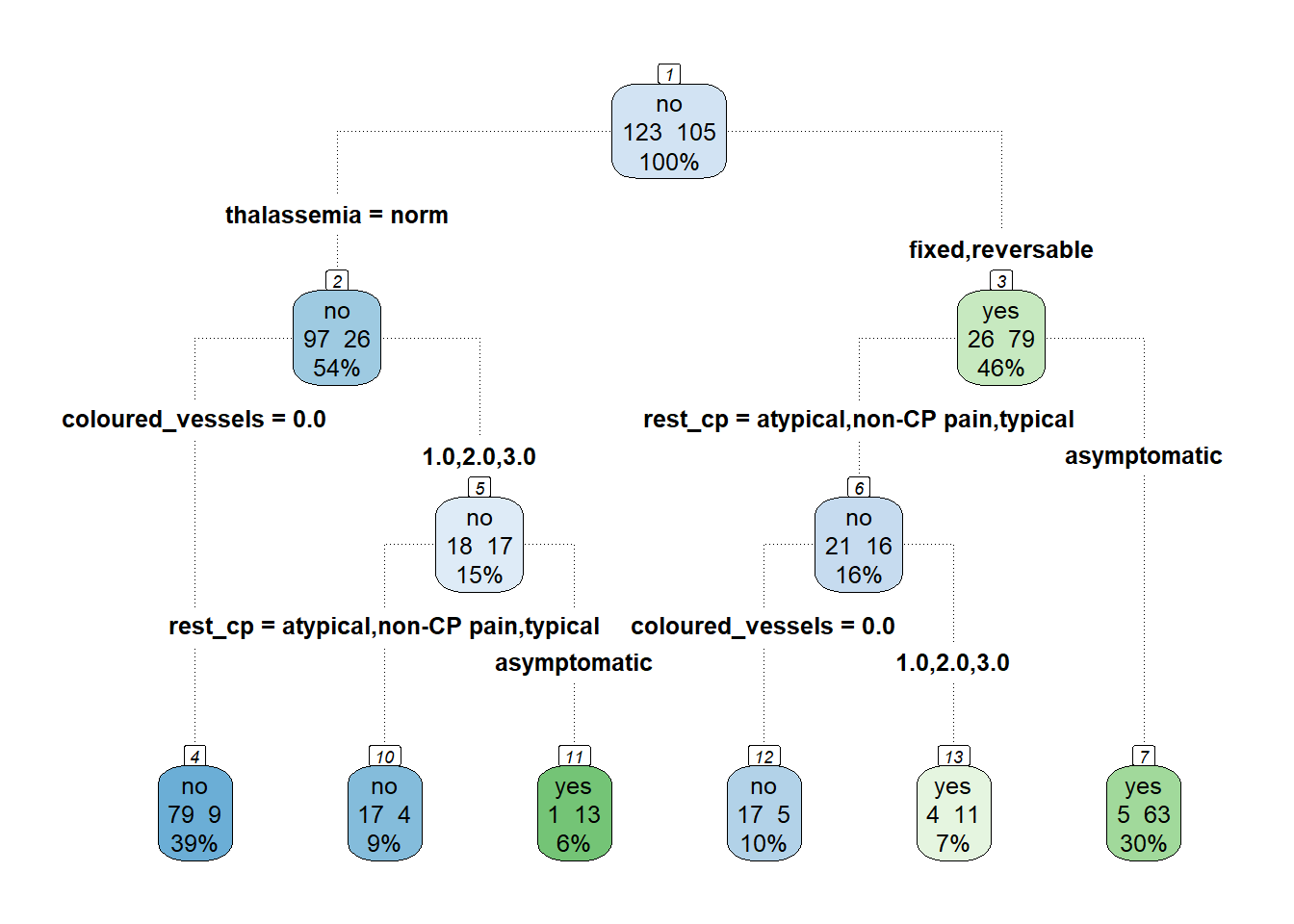
Reading the tree plot
Going down the tree from the root node will reveal the criteria to reach the terminal node and the predicted outcome. For instance looking at the extreme left branches, when the observation has thalassemia which is normal thalassemia= nomral and zero coloured vessels colour_vessesls=0.0, the predicted outcome is expected to be no heart disease.
Variable importance
The decision tree plots shows that thalassemia thalassemia, resting chest pain rest_cp, number of coloured vessels during angiogram coloured_vessels were used to split the nodes but that does not quantify which feature is more important. There may also be others variables that are important but were not used for splitting.
We can obtain the variable importance from dt_model$fit$variable.importance
dt_model$fit$variable.importance## thalassemia rest_cp coloured_vessels
## 33.157534 22.488277 22.037743
## ex_maxHR ex_STdepression_dur ex_STpeak
## 16.899032 16.676289 13.035905
## sex ex_cp rest_bp
## 9.473581 6.135384 2.919514
## age
## 2.913949However, values are in absolute terms. In other words the values do not indicate the contribution of each variable to the overall model importance. We need the values of variable importance to be in relative term. We achieve this by scaling the sum of all importance to 100.
round(100 * dt_model$fit$variable.importance / sum(dt_model$fit$variable.importance),0)## thalassemia rest_cp coloured_vessels
## 23 15 15
## ex_maxHR ex_STdepression_dur ex_STpeak
## 12 11 9
## sex ex_cp rest_bp
## 7 4 2
## age
## 2This calculated relative variable importance matches the results provided by summary(dt_model$fit).
summary(dt_model$fit) ## Call:
## rpart::rpart(formula = formula, data = data, maxdepth = ~30,
## minsplit = ~20)
## n= 228
##
## CP nsplit rel error xerror xstd
## 1 0.50476190 0 1.0000000 1.0000000 0.07167876
## 2 0.05714286 1 0.4952381 0.6095238 0.06461825
## 3 0.01000000 5 0.2666667 0.4000000 0.05574737
##
## Variable importance
## thalassemia rest_cp coloured_vessels
## 23 15 15
## ex_maxHR ex_STdepression_dur ex_STpeak
## 12 11 9
## sex ex_cp rest_bp
## 7 4 2
## age
## 2
##
## Node number 1: 228 observations, complexity param=0.5047619
## predicted class=no expected loss=0.4605263 P(node) =1
## class counts: 123 105
## probabilities: 0.539 0.461
## left son=2 (123 obs) right son=3 (105 obs)
## Primary splits:
## thalassemia splits as RLR, improve=33.15753, (0 missing)
## rest_cp splits as RLLL, improve=32.34309, (0 missing)
## coloured_vessels splits as LRRR, improve=30.87933, (0 missing)
## ex_STdepression_dur < 1.7 to the left, improve=23.83405, (0 missing)
## ex_maxHR < 146.5 to the right, improve=21.25488, (0 missing)
## Surrogate splits:
## ex_maxHR < 150.5 to the right, agree=0.689, adj=0.324, (0 split)
## ex_STdepression_dur < 0.85 to the left, agree=0.684, adj=0.314, (0 split)
## ex_STpeak splits as RRL, agree=0.684, adj=0.314, (0 split)
## sex splits as LR, agree=0.671, adj=0.286, (0 split)
## coloured_vessels splits as LRRR, agree=0.667, adj=0.276, (0 split)
##
## Node number 2: 123 observations, complexity param=0.05714286
## predicted class=no expected loss=0.2113821 P(node) =0.5394737
## class counts: 97 26
## probabilities: 0.789 0.211
## left son=4 (88 obs) right son=5 (35 obs)
## Primary splits:
## coloured_vessels splits as LRRR, improve=7.363325, (0 missing)
## rest_cp splits as RLLR, improve=6.673894, (0 missing)
## ex_STdepression_dur < 1.85 to the left, improve=6.430208, (0 missing)
## ex_maxHR < 128 to the right, improve=4.995432, (0 missing)
## age < 58.5 to the left, improve=4.834755, (0 missing)
## Surrogate splits:
## age < 68.5 to the left, agree=0.756, adj=0.143, (0 split)
## ex_STdepression_dur < 1.7 to the left, agree=0.748, adj=0.114, (0 split)
## rest_cp splits as LLLR, agree=0.732, adj=0.057, (0 split)
## ex_maxHR < 111.5 to the right, agree=0.732, adj=0.057, (0 split)
##
## Node number 3: 105 observations, complexity param=0.05714286
## predicted class=yes expected loss=0.247619 P(node) =0.4605263
## class counts: 26 79
## probabilities: 0.248 0.752
## left son=6 (37 obs) right son=7 (68 obs)
## Primary splits:
## rest_cp splits as RLLL, improve=11.696940, (0 missing)
## coloured_vessels splits as LRRR, improve= 7.761005, (0 missing)
## ex_maxHR < 143.5 to the right, improve= 5.062585, (0 missing)
## ex_STdepression_dur < 0.85 to the left, improve= 4.609524, (0 missing)
## ex_cp splits as LR, improve= 4.160173, (0 missing)
## Surrogate splits:
## ex_maxHR < 171.5 to the right, agree=0.714, adj=0.189, (0 split)
## ex_cp splits as LR, agree=0.714, adj=0.189, (0 split)
## ex_STdepression_dur < 0.85 to the left, agree=0.695, adj=0.135, (0 split)
## age < 65.5 to the right, agree=0.676, adj=0.081, (0 split)
## coloured_vessels splits as LRRR, agree=0.676, adj=0.081, (0 split)
##
## Node number 4: 88 observations
## predicted class=no expected loss=0.1022727 P(node) =0.3859649
## class counts: 79 9
## probabilities: 0.898 0.102
##
## Node number 5: 35 observations, complexity param=0.05714286
## predicted class=no expected loss=0.4857143 P(node) =0.1535088
## class counts: 18 17
## probabilities: 0.514 0.486
## left son=10 (21 obs) right son=11 (14 obs)
## Primary splits:
## rest_cp splits as RLLL, improve=9.152381, (0 missing)
## rest_bp < 139 to the right, improve=3.400244, (0 missing)
## ex_cp splits as LR, improve=2.765714, (0 missing)
## ex_STdepression_dur < 0.85 to the left, improve=2.550932, (0 missing)
## sex splits as LR, improve=2.519048, (0 missing)
## Surrogate splits:
## ex_cp splits as LR, agree=0.771, adj=0.429, (0 split)
## rest_bp < 115 to the right, agree=0.714, adj=0.286, (0 split)
## ex_maxHR < 118.5 to the right, agree=0.714, adj=0.286, (0 split)
## ex_STdepression_dur < 0.85 to the left, agree=0.714, adj=0.286, (0 split)
## ex_STpeak splits as RRL, agree=0.714, adj=0.286, (0 split)
##
## Node number 6: 37 observations, complexity param=0.05714286
## predicted class=no expected loss=0.4324324 P(node) =0.1622807
## class counts: 21 16
## probabilities: 0.568 0.432
## left son=12 (22 obs) right son=13 (15 obs)
## Primary splits:
## coloured_vessels splits as LRRR, improve=4.568223, (0 missing)
## ex_maxHR < 143 to the right, improve=2.836765, (0 missing)
## ex_STdepression_dur < 1.95 to the left, improve=2.058714, (0 missing)
## rest_cp splits as -RRL, improve=1.929404, (0 missing)
## rest_bp < 122 to the left, improve=1.630111, (0 missing)
## Surrogate splits:
## rest_cp splits as -LRL, agree=0.703, adj=0.267, (0 split)
## ex_STdepression_dur < 1.95 to the left, agree=0.703, adj=0.267, (0 split)
## age < 67.5 to the left, agree=0.676, adj=0.200, (0 split)
## ex_maxHR < 146.5 to the right, agree=0.676, adj=0.200, (0 split)
## rest_bp < 124.5 to the left, agree=0.622, adj=0.067, (0 split)
##
## Node number 7: 68 observations
## predicted class=yes expected loss=0.07352941 P(node) =0.2982456
## class counts: 5 63
## probabilities: 0.074 0.926
##
## Node number 10: 21 observations
## predicted class=no expected loss=0.1904762 P(node) =0.09210526
## class counts: 17 4
## probabilities: 0.810 0.190
##
## Node number 11: 14 observations
## predicted class=yes expected loss=0.07142857 P(node) =0.06140351
## class counts: 1 13
## probabilities: 0.071 0.929
##
## Node number 12: 22 observations
## predicted class=no expected loss=0.2272727 P(node) =0.09649123
## class counts: 17 5
## probabilities: 0.773 0.227
##
## Node number 13: 15 observations
## predicted class=yes expected loss=0.2666667 P(node) =0.06578947
## class counts: 4 11
## probabilities: 0.267 0.733Conclusion
One way to explain machine learning techniques is by using models which are already interpretable by themselves such as logistic regression which was covered in a past post and decision tree which was covered in this post. In the subsequent posts, we will use post-hoc analysis to comprehend machine learning algorithms.